K-Means, GMM e DBSCAN: Explorando Diferentes Abordagens de Clustering

A análise de dados financeiros frequentemente lida com grandes volumes de informações. O desafio é identificar padrões significativos em meio a tanta complexidade. É aí que entra o clustering, uma técnica poderosa de machine learning que agrupa dados semelhantes, ajudando analistas a tomar decisões mais informadas.

1. K-Means: A Abordagem Simples e Direta

O K-Means é tipo o arroz com feijão do clustering: popular, básico e eficiente. A lógica é dividir o conjunto de dados em K grupos, onde cada grupo tem dados parecidos entre si.

Como o K-Means Funciona?

1. Primeiro, você escolhe um número K de grupos.

2. Inicializa K centróides (centros de grupo) de forma aleatória.

3. Atribui cada ponto ao centróide mais próximo.

4. Atualiza os centróides como a média dos pontos do grupo.

5. E repete o processo até que os centróides estejam de boa (sem grandes mudanças).

   
   

Aplicação em Finanças

Na prática, o K-Means pode segmentar ações de acordo com sua volatilidade e retorno. Imagina organizar as ações em grupos como “alto risco/alto retorno” e “baixo risco/baixo retorno”. Dá para construir portfólios mais equilibrados com esses grupos!

A maior vantagem do K-Means é a sua simplicidade e eficiência. Mas, como tudo na vida, ele tem suas desvantagens: é super sensível a outliers, aqueles pontos fora da curva, e precisa que você escolha o número de grupos (K) logo de cara, o que nem sempre é fácil.

2. GMM (Gaussian Mixture Models): A Suavidade Estatística

O GMM (Gaussian Mixture Models) é para quem quer mais finesse. Ele não pressupõe que todos os grupos sejam redondinhos e de tamanhos iguais como o K-Means. Então, se você está lidando com grupos de formas variadas, o GMM pode ser sua melhor aposta.

Como o GMM Funciona?

O GMM modela os dados como uma combinação de várias distribuições Gaussianas. Em vez de colocar um ponto em um grupo específico, ele calcula a probabilidade de cada ponto pertencer a cada grupo, permitindo maior flexibilidade na forma e tamanho dos grupos.

Aplicação em Finanças

O GMM é ótimo para detectar diferentes regimes de mercado. Por exemplo, ele consegue identificar momentos de alta e baixa volatilidade em séries temporais, ajudando traders a ajustarem suas estratégias conforme o clima do mercado.

Com o GMM, você ganha flexibilidade para lidar com grupos de formas variadas e sobrepostas. Por outro lado, ele é mais complexo, consome mais recursos e exige que você defina o número de distribuições Gaussianas, o que pode ser um quebra-cabeça.

3. DBSCAN: Uma Abordagem Baseada em Densidade

Agora, se você está cansado de definir números de grupos, conheça o DBSCAN (Density-Based Spatial Clustering of Applications with Noise). Ele funciona agrupando pontos próximos e ignorando os pontos isolados, que são considerados outliers.

Cena real de um “outlier” tentando trocar uma ideia com o DBSCAN.

Como o DBSCAN Funciona?

1. Primeiro, você define a distância mínima (epsilon) e o número mínimo de pontos para formar um grupo.

2. Identifica os pontos centrais, que têm pelo menos o número mínimo de vizinhos dentro de epsilon.

3. Agrupa pontos densamente conectados e marca os que não se encaixam como outliers.

   
   

Aplicação em Finanças

O DBSCAN é muito bom para detectar anomalias, como picos de volatilidade ou eventos estranhos de negociação. Ele também segmenta clusters com tamanhos e formas irregulares, perfeito para ações que têm comportamentos esquisitos por causa de eventos externos.

Uma das grandes vantagens desse método é que ele não fica te pedindo para adivinhar o número de grupos logo de cara, o que é um baita alívio! Além disso, ele tem um olfato aguçado para detectar outliers, como aquele colega que sempre aparece com um projeto maluco. Por outro lado, ele é meio exigente: fica super sensível aos parâmetros epsilon e ao número mínimo de pontos, como se fosse uma criança manhosa comendo brócolis. E, para complicar um pouco mais, ele se perde bonito quando tem que lidar com muitos dados, tipo aquela planilha de Excel cheia de colunas que ninguém entende.

Comparação das Abordagens

Qual Abordagem Escolher?

A escolha entre K-Means, GMM e DBSCAN depende do seu cenário e do que você quer descobrir. Se você já tem um número claro de grupos e busca simplicidade, o K-Means é a sua praia. Se os grupos são mais complexos ou têm sobreposição, o GMM é o ideal. E, se a detecção de outliers e clusters de formas variadas é o seu foco, vai de DBSCAN sem medo!

No fim das contas, o mundo financeiro é cheio de padrões esperando para serem descobertos. Entender qual técnica de clustering usar em cada situação pode fazer toda a diferença. Como diria Mark Twain, “A história não se repete, mas rima”. Do mesmo jeito, os dados financeiros podem não se repetir perfeitamente, mas têm padrões semelhantes esperando para serem descobertos.

Então, na próxima vez que estiver lidando com um mar de dados financeiros, experimente essas técnicas e veja como elas podem te ajudar a encontrar padrões escondidos no meio do caos dos mercados! 🚀

Aqui vai um exemplo em Python 👇

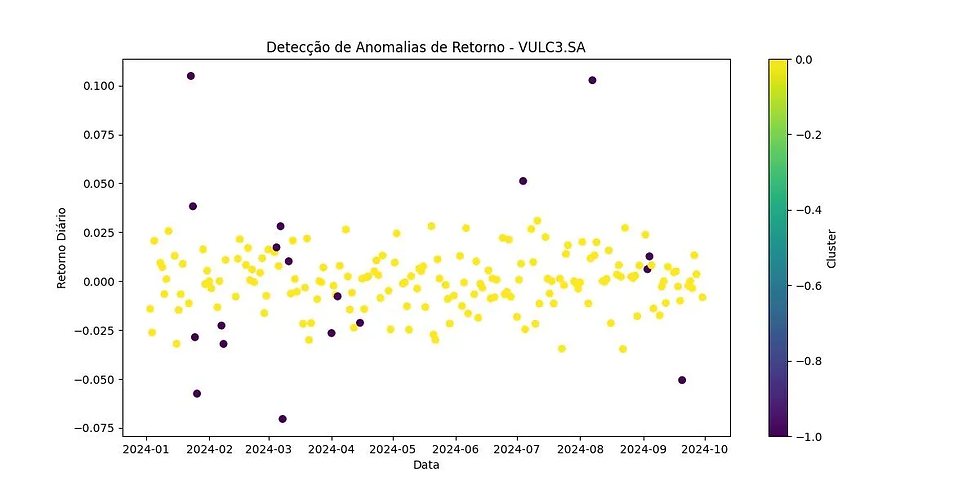
No gráfico gerado, cada ponto representa um dia. Os pontos marcados como anômalos (em cores distintas, com rótulo Cluster = -1) indicam dias onde os retornos/volumes foram significativamente diferentes do comportamento normal, o que pode sinalizar um evento incomum como uma grande variação de preço devido a notícias inesperadas, resultados financeiros, ou outros eventos.

Os parâmetros eps e min_samples são cruciais. Se você definir um valor de eps muito grande, mais pontos serão agrupados, resultando em menos anomalias. Por outro lado, um valor pequeno pode classificar muitos pontos como anômalos. Uma boa prática é ajustar esses parâmetros com base na análise exploratória dos dados.

Espero que esse exemplo tenha ajudado a entender como o DBSCAN pode ser aplicado na análise financeira para detectar anomalias! Experimente usar diferentes ações e ajustar os parâmetros para ver como os resultados mudam. 🚀